Notes

第10章 量子跃迁

10.1 量子态随时间的演化

Hamilton量不含时的体系

如果Hamilton量不含时，即 $\frac{\partial \hat{H}}{\partial t} = 0$ ，则体系能量守恒，若已知初态为 $| \psi(0) \rangle$ ，则量子态随时间的演化为

$$| \psi(t) \rangle = \hat{U}(t) | \psi(0) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} | \psi(0) \rangle$$

将初态按能量本征态展开，即

$$| \psi(0) \rangle = \sum_n a_n | \psi_n \rangle$$

其中

$$\hat{H} | \psi_n \rangle = E_n | \psi_n \rangle \ \ \ a_n = \langle \psi_n | \psi(0) \rangle \kern 1em (不显含时间)$$

则 $t$ 时刻的量子态可以表示为

$$| \psi(t) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t} \sum_n a_n | \psi_n \rangle = \sum_n a_n \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle$$

如果初态为能量本征态，即

$$| \psi(0) \rangle = | \psi_k \rangle$$

则 $t$ 时刻的量子态为

$$| \psi(t) \rangle = \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_kt} | \psi_k \rangle$$

这种量子态，称为定态；若初态不是能量本征态，则称为非定态。

Hamilton量含时体系的量子跃迁的微扰论

量子跃迁及一级近似

对于含时Hamilton量 $\hat{H}(t)$ 所描述的体系，能量是不守恒的，Hamilton量可以分解为不含时部分与含时微扰两部分

$$\hat{H}(t) = \hat{H}_0 + \hat{H}'(t)$$

若体系初态为 $\hat{H}_0$ 的本征态 $| \psi_k \rangle$ ，则体系不能保持在原有的本征态，而是将变成各本征态的叠加态，即

$$| \psi(t) \rangle = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle$$

再次测量时，有一定的概率离开初态而处于其它定态，这种现象叫做量子跃迁。

在一级近似下，从 $\psi_k$ 态跃迁到 $\psi_{k'}$ 态的跃迁振幅为

$$C_{k'k}(t) = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t H'$${k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau

其中

$$H'$${k'k}(t) = \langle k' | \hat{H}'(t) | k \rangle \ \ \ \omega{k'k} = \frac{E_{k'}-E_k}{\hbar}

对于 $k' \ne k$ 的情况，即末态不同于初态，有

$$C_{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'$${k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau

跃迁概率为

$$P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{1}{\hbar^2} \left| \int_0^t H'$${k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau \right|^2

单位时间内的跃迁概率，即跃迁速率为

$$w_{k'k}(t) = \frac{\mathrm{d}}{\mathrm{d}t} |C_{k'k}(t)|^2 = \frac{1}{\hbar^2} \frac{\mathrm{d}}{\mathrm{d}t} \left| \int_0^t H'$${k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau \right|^2

跃迁振幅推导

$$\begin{cases} | \psi(t) \rangle = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle \ C_{nk}(0) = \delta_{nk} \end{cases}$$

将 $t$ 时刻的量子态表达式代入Schrödinger方程，可得

$$\mathrm{i}\hbar \frac{\partial}{\partial t} \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle = \left( \hat{H}$$0 + \hat{H}'(t) \right) \sum_n C{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | \psi_n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \left[ \frac{\partial}{\partial t} C_{nk}(t) \right] \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle + \mathrm{i}\hbar \sum_n C_{nk}(t) \left[ \frac{\partial}{\partial t} \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \right] | n \rangle \ \ \ = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}0 | n \rangle + \sum_n C{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \dot{C}{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle + \sum_n C{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} E_n | n \rangle \ \ \ = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} E_n | n \rangle + \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \sum_n \dot{C}{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} | n \rangle = \sum_n C{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \hat{H}'(t) | n \rangle

对上式左乘 $\langle k' |$ ，利用本征函数的正交归一性，可得

$$\mathrm{i}\hbar \sum_n \dot{C}$${nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | n \rangle = \sum_n C{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \dot{C}{k'k}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E{k'}t} = \sum_n C_{nk}(t) \mathrm{e}^{-\frac{\mathrm{i}}{\hbar}E_nt} \langle k' | \hat{H}'(t) | n \rangle \ \Downarrow \ \mathrm{i}\hbar \dot{C}{k'k}(t) = \sum_n C{nk}(t) \mathrm{e}^{\frac{\mathrm{i}}{\hbar}(E_{k'}-E_n)t} \langle k' | \hat{H}'(t) | n \rangle

记

$$H'$${k'n}(t) = \langle k' | \hat{H}'(t) | n \rangle \ \ \ \omega{k'n} = \frac{E_{k'}-E_n}{\hbar}

则跃迁振幅满足方程

$$\begin{cases} \mathrm{i}\hbar \dot{C}$${k'k}(t) = \sum_n H'{k'n}(t) \mathrm{e}^{\mathrm{i}\omega_{k'n}t} C_{nk}(t) \ C_{k'k}(0) = \delta_{k'k} \end{cases}

方程两边对 $t$ 积分可得

$$C_{k'k}(t) = C_{k'k}(0) + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'$${k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} C_{nk}(\tau) \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} C_{nk}(\tau) \mathrm{d}\tau

该积分方程可迭代求解，即

$$C_{k'k}(t) \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'$${k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} \left[ \delta_{nk} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega{nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} \delta_{nk}\mathrm{d}\tau \ \ \ + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} \left[ \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega{nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau \ \ \ = \delta_{k'k} + \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau \ \ \ + \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_n H'{k'n}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'n}\tau} \left[ \frac{1}{\mathrm{i}\hbar} \int_0^t \sum_m H'{nm}(\tau') \mathrm{e}^{\mathrm{i}\omega{nm}\tau'} C_{mk}(\tau') \mathrm{d}\tau' \right] \mathrm{d}\tau

故零级近似

$$C^{(0)}$${k'k}(t) = \delta{k'k}

一级近似

$$C^{(1)}$${k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau

对简并的处理

初态有简并

对初态按各简并的各本征态展开，按照各本征态出现的概率对各本征态向末态的跃迁概率求加权平均和。

末态有简并

对向末态的各简并态的跃迁概率求和。

量子跃迁理论与定态微扰论的关系

10.2 周期微扰与常微扰

周期微扰

考虑周期微扰

$$\hat{H}'(t) = H' \mathrm{e}^{-\mathrm{i}\omega t}$$

则在 $t$ 时刻体系从初态 $| k \rangle$ 跃迁到末态 $| k' \rangle \ (k' \ne k)$ 的跃迁振幅为

$$C_{k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'$${k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau \ \ \ = \frac{1}{\mathrm{i}\hbar} \int_0^t \langle k' | H' | k \rangle \mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)\tau} \mathrm{d}\tau \ \ \ = \frac{1}{\mathrm{i}\hbar} \langle k' | H' | k \rangle \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\mathrm{i}(\omega_{k'k}-\omega)}

记 $H'_{k'k} = \langle k' | H' | k \rangle$ ，则跃迁概率

$$P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{4|H'$${k'k}|^2}{\hbar^2} \left{ \frac{\sin[\omega{k'k}-\omega)t/2]}{\omega_{k'k}-\omega} \right}^2

利用 $\lim_{\alpha\to\infty} \frac{\sin^2\alpha x}{x^2} = \pi\alpha\delta(x)$ ，可得当 $(\omega_{k'k} - \omega)t \gg 1$ 时，

$$P_{k'k}(t) = \frac{2\pi t}{\hbar^2} |H'$${k'k}|^2 \delta(\omega{k'k}-\omega)

跃迁速率为

$$w_{k'k} = \frac{\partial}{\partial t} P_{k'k}(t) = \frac{2\pi}{\hbar^2} |H'$${k'k}|^2 \delta(\omega{k'k}-\omega) \ \ \ = \frac{2\pi}{\hbar} |H'{k'k}|^2 \delta(E{k'}-E_k-\hbar\omega)

由此可见，如果周期微扰持续的时间足够长，即远大于体系的内禀特征时间，则跃迁速率将与时间无关。

上述结果适用于分立谱的情况，对于连续谱，有意义的是计算跃迁到能量 $E_{k'}$ 附近全部可能末态的总概率，即设末态的态密度为 $\rho(E_{k'})$ ，则总跃迁概率

$$P_{\text{total}}(t) = \int P_{k'k}(t) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi t}{\hbar} |H'$${k'k}|^2 \delta(E{k'}-E_k-\hbar\omega) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi t}{\hbar} |H'{k'k}|^2 \rho(E{k} + \hbar\omega)

总跃迁速率

$$w_{\text{total}} = \frac{\partial}{\partial t} P_{\text{total}}(t) = \frac{2\pi}{\hbar} |H'$${k'k}|^2 \rho(E{k} + \hbar\omega)

常微扰

只在一段时间间隔（如 $0 \sim T$ ）内，对体系施加与时间无关的微扰，称为常微扰，即

$$\hat{H}'(t) = H' [\theta(t) - \theta(t-T)]$$

其中 $\theta(t)$ 为阶梯函数，定义为

$$\theta(t) = \begin{cases} 0 , & t<0 \ 1 , & t>0 \end{cases}$$

故

$$\hat{H}'(t) = \begin{cases} H' , & 0 \le t < T \ 0 , & t > T \end{cases}$$

则一级近似下的跃迁振幅为

$$C^{(1)}$${k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int{-\infty}^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{H'{k'k}(t)\mathrm{e}^{\mathrm{i}\omega{k'k}t}}{\hbar\omega_{k'k}} + \int_{-\infty}^t \frac{\partial H'{k'k}(\tau)}{\partial \tau} \frac{\mathrm{e}^{\mathrm{i}\omega{k'k}\tau}}{\hbar\omega_{k'k}} \mathrm{d}\tau \ \ \ = -\frac{H'{k'k}(t)\mathrm{e}^{\mathrm{i}\omega{k'k}t}}{\hbar\omega_{k'k}} + \int_{-\infty}^t H'{k'k} [\delta(\tau) - \delta(\tau-T)] \frac{\mathrm{e}^{\mathrm{i}\omega{k'k}\tau}}{\hbar\omega_{k'k}} \mathrm{d}\tau

当 $t>T$ 后

$$C^{(1)}$${k'k}(t) = \frac{H'{k'k}}{\hbar\omega_{k'k}} \left( 1 - \mathrm{e}^{\mathrm{i}\omega_{k'k}T} \right)

故 $k' \ne k$ 的跃迁概率为

$$P_{k'k}(t) = |C_{k'k}(t)|^2 = \frac{|H'$${k'k}|^2}{\hbar^2} \frac{\sin^2(\omega{k'k}T/2)}{(\omega_{k'k}/2)^2}

利用 $\lim_{\alpha\to\infty} \frac{\sin^2\alpha x}{x^2} = \pi\alpha\delta(x)$ ，可得当常微扰作用的时间间隔足够长，即 $\omega_{k'k}T \gg 1$ 时，

$$P_{k'k}(t) = \frac{2\pi T}{\hbar^2} |H'$${k'k}|^2 \delta(\omega{k'k}) = \frac{2\pi T}{\hbar} |H'{k'k}|^2 \delta(E{k'} - E_k)

跃迁速率为

$$w_{k'k} = \frac{P_{k'k}(t)}{T} = \frac{2\pi}{\hbar} |H'$${k'k}|^2 \delta(E{k'}-E_k)

由此可见，如果常微扰作用的时间足够长，即远大于体系的内禀特征时间，则跃迁速率将与时间无关。

上述结果适用于分立谱的情况，对于连续谱，有意义的是计算跃迁到能量 $E_{k'}$ 附近全部可能末态的总概率，即设末态的态密度为 $\rho(E_{k'})$ ，则总跃迁概率

$$P_{\text{total}}(t) = \int P_{k'k}(t) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi T}{\hbar} |H'$${k'k}|^2 \delta(E{k'}-E_k) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi T}{\hbar} |H'{k'k}|^2 \rho(E{k})

总跃迁速率（Fermi黄金规则）

$$w_{\text{total}} = \int w_{k'k} \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \int \frac{2\pi}{\hbar} |H'$${k'k}|^2 \delta(E{k'}-E_k) \rho(E_{k'}) \mathrm{d}E_{k'} \ \ \ = \frac{2\pi}{\hbar} |H'{k'k}|^2 \rho(E{k})

10.3 光的吸收与辐射

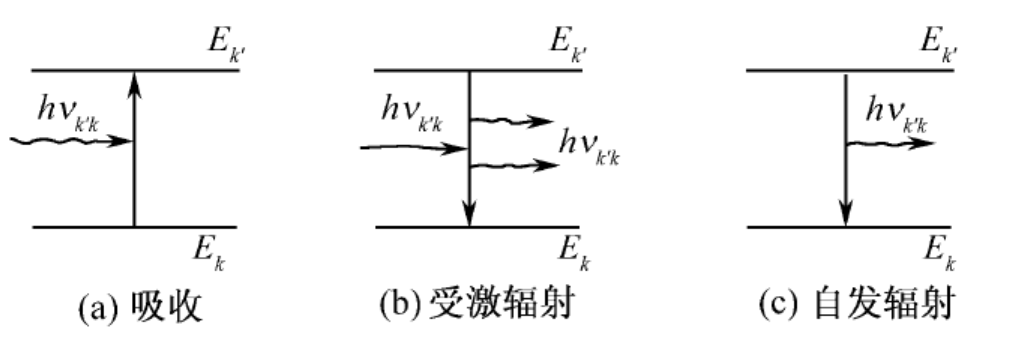
在光的照射下，原子可能吸收光而从低能级跃迁到较高能级，称为光的吸收(obsorption)；或从较高能级跃迁到较低能级并放出光，称为受激辐射(induced radiation)；如果原子本来处于激发能级，即使没有外界光的照射，也可能跃迁到某些较低能级而放出光来，称为自发辐射(spontaneous radiation)。

注：本节均使用高斯单位制CGS。

光的吸收与受激辐射

电偶极跃迁及其速率

先假设入射光为平面单色光，其电磁场强度分别为

$$\vec{E} = \vec{E}_0 \cos(\omega t - \vec{k} \cdot \vec{r}) \ \ \ \vec{B} = \vec{k} \times \frac{\vec{E}}{|\vec{k}|}$$

由于在原子中，电子的速度 $v \ll c$ ，故磁场对电子的作用 $\left| \frac{e}{c} \vec{v} \times \vec{B} \right|$ 远小于电场的作用 $\left| e \vec{E} \right|$ ，同时，对于可见光与紫外光，波长 $\lambda$ 远大于Bohr半径 $a$ ，故在原子大小范围中， $\vec{k} \cdot \vec{r} \sim 2\pi a / \lambda \ll 1$ ，故电场随空间的变化极微，可视为匀强电场，故

$$\vec{E} = \vec{E}_0 \cos(\omega t)$$

入射可见光对于原子中电子的作用可表示为

$$\hat{H}'(t) = - \vec{D} \cdot \vec{E} = - \vec{D} \cdot \vec{E}_0 \cos(\omega t) = W \cos(\omega t)$$

其中

$$W = - \vec{D} \cdot \vec{E}_0 , \kern 2em \vec{D} = -e \vec{r} (电偶极矩)$$

电偶极矩与电场作用引起的跃迁称为电偶极跃迁。

在一级近似下，对于从 $E_k \to E_{k'} \kern 1em (E_{k'}>E_k)$ 的跃迁，跃迁振幅

$$C^{(1)}$${k'k}(t) = -\frac{W{k'k}}{2\hbar} \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega}

跃迁概率

$$P_{k'k}(t) = \left| C^{(1)}$${k'k}(t) \right|^2 = \frac{|W{k'k}|^2}{4\hbar^2} \frac{\sin^2[(\omega_{k'k}-\omega)t/2]}{[(\omega_{k'k}-\omega)/2]^2}

当时间足够长时，只有 $\omega \approx \omega_{k'k}$ 的入射光才对跃迁有明显贡献，此时

$$P_{k'k}(t) = \frac{\pi t}{4\hbar^2} |W_{k'k}|^2\ \delta[(\omega_{k'k}-\omega)/2]$$

跃迁速率

$$w_{k'k} = \frac{\mathrm{d}}{\mathrm{d}t} P_{k'k} = \frac{\pi}{2\hbar^2} |W_{k'k}|^2\ \delta(\omega_{k'k}-\omega) \ \ \ = \frac{\pi}{2\hbar^2} |\vec{D}$${k'k} \cdot \vec{E}0|^2\ \delta(\omega{k'k}-\omega) \ \ \ = \frac{\pi}{2\hbar^2} |\vec{D}{k'k}|^2 E_0^2\ \cos^2\theta\ \delta(\omega_{k'k}-\omega)

其中 $\theta$ 为 $\vec{D}_{k'k}$ 与 $E_0$ 的夹角。如果入射光为非偏振光，即 $\vec{E}_0$ 的方向是完全无规定的，故 $\cos^2\theta$ 应取为对空间各方向的平均值

$$\overline{\cos^2\theta} = \frac{1}{4\pi} \int \mathrm{d}\Omega\ \cos^2\theta \ \ \ = \frac{1}{4\pi} \int_{0}^{2\pi} \mathrm{d}\varphi \int_{0}^{\pi} \sin\theta \cos^2\theta \mathrm{d}\theta = \frac13$$

故非偏振光的跃迁速率

$$w_{k'k} = \frac{\pi}{6\hbar^2} |\vec{D}$${k'k}|^2 E_0^2\ \delta(\omega{k'k}-\omega)

对于非单色光，用 $\rho(\omega)$ 表示角频率为 $\omega$ 的电磁辐射场的能量密度对时间的平均值，可得

$$\rho(\omega) = \frac{1}{8\pi} \overline{(E^2+B^2)} \ \ \ = \frac{1}{4\pi} \overline{E^2} \ \ \ = \frac{E_0^2(\omega)}{4\pi} \frac{1}{T} \int_0^T \cos^2 \omega t\ \mathrm{d}t \ \ \ = \frac{1}{8\pi} E_0^2(\omega) \ \Downarrow \ E_0^2(\omega) = 8\pi\rho(\omega)$$

故非单色光的跃迁速率

$$w_{\text{total}} = \int_{-\infty}^{+\infty} w_{k'k}\ \mathrm{d}\omega \ \ \ = \int_{-\infty}^{+\infty} \frac{\pi}{6\hbar^2} |\vec{D}$${k'k}|^2 E_0^2(\omega)\ \delta(\omega{k'k}-\omega) \mathrm{d}\omega \ \ \ = \frac{4\pi^2}{3\hbar^2} |\vec{D}{k'k}|^2 \int{-\infty}^{+\infty} \rho(\omega) \delta(\omega_{k'k}-\omega) \mathrm{d}\omega \ \ \ = \frac{4\pi^2}{3\hbar^2} |\vec{D}{k'k}|^2 \rho(\omega{k'k}) \ \ \ = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}{k'k}|^2 \rho(\omega{k'k})

其中 $|\vec{r}${k'k}|^2 = |x{k'k}|^2 + |y_{k'k}|^2 + |z_{k'k}|^2 ，这三个分量矩阵元至少有一个不为零时，跃迁才可能发生。

跃迁的快慢与入射光中频率为 $\omega_{k'k}$ 的光强度 $\rho(\omega_{k'k})$ 成正比，若入射光不包含频率为 $\omega_{k'k}$ 的成分，则不能引起 $E_{k} \leftrightarrow E_{k'}$ 两能级之间的跃迁。

跃迁振幅推导

把 $\hat{H}'(t)= - W \cos(\omega t)$ 代入跃迁振幅的一级微扰公式可得

$$C^{(1)}$${k'k}(t) = \frac{1}{\mathrm{i}\hbar} \int_0^t H'{k'k}(\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{\mathrm{i}\hbar} \int_0^t \cos(\omega\tau) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{2\mathrm{i}\hbar} \int_0^t (\mathrm{e}^{\mathrm{i}\omega\tau} + \mathrm{e}^{-\mathrm{i}\omega\tau}) \mathrm{e}^{\mathrm{i}\omega_{k'k}\tau} \mathrm{d}\tau \ \ \ = -\frac{W_{k'k}}{2\hbar} \left[ \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}+\omega)t}-1}{\omega_{k'k}+\omega} + \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega} \right]

对于可见光以及紫外光， $\omega$ 很大，故括号中的第一项产生的贡献可以忽略，只有当 $\omega \approx \omega_{k'k}$ 时，第二项才能有显著的贡献，故

$$C^{(1)}$${k'k}(t) = -\frac{W{k'k}}{2\hbar} \frac{\mathrm{e}^{\mathrm{i}(\omega_{k'k}-\omega)t}-1}{\omega_{k'k}-\omega}

选择定则

理论描述

电偶极跃迁的角动量选择定则为：初末态量子数满足

$$\Delta l = \pm1 ,\kern 1em \Delta m_l = 0, \pm 1 , \kern 1em \Delta m_s = 0$$

其中对于电场平行于 $z$ 轴的偏振光， $\Delta m_l = 0$ ，对于电场平行于 $x$ 轴或 $y$ 轴的偏振光， $\Delta m_l = \pm1$ 。

原子的宇称 $\pi = (-1)^l$ ，故只有初末态宇称不同，才可能发生电偶极跃迁。

如果使用耦合表象，则选择定则表述为

$$\Delta l = \pm1 ,\kern 1em \Delta j = 0, \pm 1 , \kern 1em \Delta m_j = 0, \pm1$$

证明

考虑矩阵元 $\vec{r}_{k'k}$ ，因为其与自旋无关，故

$$\langle k' | \vec{r} | k \rangle = \langle n'l'm_l's'm_s' | \vec{r} | nlm_lsm_s \rangle \ \ \ = \langle n'l'm_l' | \vec{r} | nlm_l \rangle \langle \frac12m_s' | \frac12m_s \rangle \ \ \ = \langle n'l'm_l' | \vec{r} | nlm_l \rangle \delta_{m_s'm_s}$$

故只有 $m_s' = m_s$ 时，即自旋方向不变，跃迁才可能发生，接下来的讨论基于此条件。

对于电场平行于 $z$ 轴的偏振光，只有矩阵元 $z_{k'k}$ 对跃迁有贡献

$$z_{k'k} = \langle n'l'm_l' | r\cos\theta | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}$${l'm_l'}(\theta,\varphi) | r\cos\theta | R{nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = (R{n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \cos\theta \mathrm{Y}{lm_l})

其中 $(R_{n'l'} , r R_{nl}) \ne 0$ ，考虑球谐函数的递推关系式

$$\cos\theta\mathrm{Y}$${l,m_l} = \sqrt{\frac{(l+1)^2-m_l^2}{(2l+1)(2l+3)}} \mathrm{Y}{l+1,m_l} + \sqrt{\frac{l^2-m_l^2}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l}

可得

$$(\mathrm{Y}$${l'm_l'} , \cos\theta \mathrm{Y}{lm_l}) \ \ \ = \sqrt{\frac{(l+1)^2-m_l^2}{(2l+1)(2l+3)}} \delta_{l',l+1}\delta_{m_l',m_l} + \sqrt{\frac{l^2-m_l^2}{(2l-1)(2l+1)}} \delta_{l',l-1}\delta_{m_l',m_l}

故当 $\Delta l = \pm1 ,\kern 1em \Delta m_l = 0$ 时，跃迁才可能发生；

对于电场平行于 $x$ 轴的偏振光，只有矩阵元 $x_{k'k}$ 对跃迁有贡献

$$x_{k'k} = \langle n'l'm_l' | r\sin\theta\cos\varphi | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}$${l'm_l'}(\theta,\varphi) | \frac{r}{2}\sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) | R{nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = \frac12 (R{n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y}{lm_l})

其中 $(R_{n'l'} , r R_{nl}) \ne 0$ ，考虑球谐函数的递推关系式

$$\mathrm{e}^{\pm\mathrm{i}\varphi}\sin\theta\mathrm{Y}$${l,m_l} = \pm \sqrt{\frac{(l\pm m_l+1)(l\pm m_l+2)}{(2l+1)(2l+3)}} \mathrm{Y}{l+1,m_l\pm1} \mp \sqrt{\frac{(l\mp m_l)(l\mp m_l-1)}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l\pm1}

可得

$$(\mathrm{Y}$${l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}+\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y}{lm_l}) \ \ \ = \sqrt{\frac{(l+m_l+1)(l+m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l+1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l+1} \ \ \ - \sqrt{\frac{(l-m_l+1)(l-m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l-1} + \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l-1}

故当 $\Delta l = \pm1 ,\kern 1em \Delta m_l = \pm 1$ 时，跃迁才可能发生；

对于电场平行于 $y$ 轴的偏振光，只有矩阵元 $y_{k'k}$ 对跃迁有贡献

$$y_{k'k} = \langle n'l'm_l' | r\sin\theta\sin\varphi | nlm_l \rangle \ \ \ = \langle R_{n'l'}(r) \mathrm{Y}$${l'm_l'}(\theta,\varphi) | \frac{r}{2\mathrm{i}}\sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) | R{nl}(r) \mathrm{Y}{lm_l}(\theta,\varphi) \rangle \ \ \ = \frac{1}{2\mathrm{i}} (R{n'l'} , r R_{nl}) (\mathrm{Y}{l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y}{lm_l})

其中 $(R_{n'l'} , r R_{nl}) \ne 0$ ，考虑球谐函数的递推关系式

$$\mathrm{e}^{\pm\mathrm{i}\varphi}\sin\theta\mathrm{Y}$${l,m_l} = \pm \sqrt{\frac{(l\pm m_l+1)(l\pm m_l+2)}{(2l+1)(2l+3)}} \mathrm{Y}{l+1,m_l\pm1} \mp \sqrt{\frac{(l\mp m_l)(l\mp m_l-1)}{(2l-1)(2l+1)}} \mathrm{Y}_{l-1,m_l\pm1}

可得

$$(\mathrm{Y}$${l'm_l'} , \sin\theta(\mathrm{e}^{\mathrm{i}\varphi}-\mathrm{e}^{-\mathrm{i}\varphi}) \mathrm{Y}{lm_l}) \ \ \ = \sqrt{\frac{(l+m_l+1)(l+m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l+1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l+1} \ \ \ + \sqrt{\frac{(l-m_l+1)(l-m_l+2)}{(2l+1)(2l+3)}} \delta_{l+1,m_l-1} - \sqrt{\frac{(l-m_l)(l-m_l-1)}{(2l-1)(2l+1)}} \delta_{l-1,m_l-1}

故当 $\Delta l = \pm1 ,\kern 1em \Delta m_l = \pm 1$ 时，跃迁才可能发生。

自发辐射的Einstein理论

在强度为 $\rho(\omega)$ 的辐射的照射下，原子从 $k$ 态到 $k'$ 态的跃迁速率为（设 $E_{k'}>E_k$ ）

$$w_{k'k} = B_{k'k} \rho(\omega_{k'k})$$

其中吸收系数

$$B_{k'k} = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}_{k'k}|^2$$

从 $k'$ 态到 $k$ 态的跃迁速率为

$$w_{kk'} = B_{kk'} \rho(\omega_{k'k})$$

其中受激辐射系数

$$B_{kk'} = \frac{4\pi^2e^2}{3\hbar^2} |\vec{r}_{kk'}|^2$$

由于 $\hat{\vec{r}}$ 为厄米算符，则 $\vec{r}${k'k} = \vec{r}^*{kk'} ，故

$$B_{k'k} = B_{kk'}$$

即受激辐射系数等于吸收系数，他们都与入射光强度无关，只决定于原子的自身性质。

根据Boltzmann分布律，处于平衡状态时，粒子数 $n$ 与能量有关，当 $E_{k'} \ne E_k$ 时， $n_{k'} \ne n_k$ （通常情况下 $n_{k'} < n_k$ ），则